机器学习课程笔记-6

2017-04-02

Notes about Andrew Ng's Machine Learning course on Coursera-part 6

原创文章，转载请注明：转自Luozm's Blog

1 Debug the algorithm

如果在测试集上的表现很差（损失函数值非常大），应该如何改进？

获得更多训练数据（可能没有想象中管用，成本很高）
从特征集中挑选一部分特征（过拟合）
添加更多的特征（欠拟合）
调整正则化系数

1.1 Machine Learning diagnostic

诊断：进行一个测试来找出学习算法的Bug，并获得指导怎么样能最好的提升算法的性能。

2. Evaluation & Diagnosis

2.1 Evaluate the hypothesis

划分训练集和测试集：

随机划分数据集为训练集和测试集（7/3）
使用训练集训练模型参数，最小化损失函数
计算测试误差（损失函数或Metrics）

2.2 Model selection

通常情况下，使用训练集来拟合参数，在训练集上的训练误差（损失函数）很可能会比实际泛化误差（generalization error）要低。

模型选择问题：

对每个可能选择的模型分别训练，得到相应的最优参数，然后分别在测试集上测试比较误差。

但问题是：这个最优的测试误差可能是对泛化误差的一个乐观估计，即：超参数的选择是基于测试集的。可能对于新的我们没见过的数据来说，这个参数选择不一定是最优的。

划分训练集、验证集和测试集：

划分训练集（training set）、交叉验证集（cross validation set/validation set）、测试集（test set），比例为6：2：2
使用训练集训练模型参数，最小化损失函数
在验证集上计算验证误差，找出最优模型
选择该模型在测试集上计算测试误差，来估计泛化误差

这样计算出的泛化误差更加可靠，因为测试集与模型选择无关。

2.3 bias vs. variance

如何诊断模型的Bias/Variance？分别画出训练误差和验证误差随超参数改变的曲线： diagnosis

训练误差较高，验证误差和测试误差相似，很可能是High Bias问题（欠拟合）
训练误差很低，验证误差远大于训练误差，很可能是High Variance问题（过拟合）

2.4 Regularization

如何正确选择正则化参数来避免bias/variance问题？

定义损失函数中含有正则化项，但在训练误差、验证误差、测试误差中不含正则化项：
尝试不同的正则化参数值，作为不同的模型训练参数
在验证集上计算验证误差，找出最优模型（正则化参数）
选择该模型在测试集上计算测试误差，来估计泛化误差

lambda-loss

2.5 Learning curves

学习曲线就是误差随训练集大小改变的曲线（正常情况）： learning curve High Bias的情况： high bias curve 此时增加获得更多训练数据可能不会有效，因为模型的复杂度不足以拟合这些数据。

High Variance的情况： high variance curve 此时增加更多训练数据有效，因为模型过拟合，更多数据可以拟合的更好。

2.6 Debug

回顾第一节中提到的问题，现在我们知道了在什么情况下应该使用哪种方法：

Getting more training examples: 解决 high variance
Trying smaller sets of features: 解决 high variance
Adding features: 解决 high bias
Adding polynomial features: 解决 high bias
Decreasing λ: 解决 high bias
Increasing λ: 解决 high variance.

neural networks 在参数的选择时，我们可以将数据集划分为训练集和验证集，然后分别画出前面说过的各种曲线（learning curves），判断模型现在可能的问题，选择对应的解决方案来处理它。

3. Machine Learning system design

在设计大型机器学习系统时，有那些注意事项呢？

3.1 EX1：Building a spam classifier

分类器的建立

选择监督学习
$x =$电子邮件的特征
$y =$是垃圾邮件（1）或者不是（0）
特征 $x$ 选择：挑选100个可以区分是否为垃圾邮件的单词：比如deal, buy, discount, andrew（姓名）, now, …
对于每封邮件，建立对应的特征向量（是否出现这个单词表中的单词）

具体步骤如下： spam classifier

如何有效的改进分类器？（最优时间分配）

你可能会在头脑风暴后列出以下选项：

收集大量数据
基于邮件标题信息（email routing information）来设计复杂的特征
基于邮件内容信息设计复杂的特征，比如：discount/discounts，deal/Dealer是否作为同一个词来对待？关于标点符号的特征？
设计复杂的算法来检测拼写错误（比如m0rtgage，med1cine，w4tches）

我们应该把时间花在最有效的改进方案上，但是哪个方案更加有效？这就要通过误差分析而不是某天早上醒来的突发奇想（我好像也有类似的举动……）来发现了。

3.2 Error Analysis

一个推荐的建立机器学习系统的流程是：

从一个可以快速实现的简单的算法（只用24小时或更少）开始，对其进行交叉检验和测试；
画出学习曲线来决定是否更多数据或者更多特征会可能对提升性能有帮助；
误差分析：人工检查算法分错的样本（在交叉验证集中），看看是否在这些错分的样本中存在一些系统的规律，这可以告诉你当前算法的缺陷并指导你如何进一步设计特征来改进算法。

EX2：Error Analysis

在交叉验证集中有500个样本，其中算法错分了100封邮件。人工检查这100个错误，并将其分类：

这些邮件属于什么类型？比如钓鱼邮件、卖仿制品、…
想想什么样的特征有可能会帮助算法来正确区分这些特定类型的样本基于这两个列表，我们可以更好的发现如何改进算法更有效，比如改进钓鱼邮件和异常符号特征可能会比较有效。

Numerical evaluation

在上面的例子中，是否应该将discount/discounts/discounted/discounting视为同一个单词呢？误差分析没办法直接告诉你答案，只有分别尝试然后比较结果才能知道。

这时需要使用Numerical evaluation（比如交叉验证误差）对使用或不使用stemming（词干提取）的算法性能分别进行测试。

3.3 Error Metrics

有些情况下，Accuracy 和 Error不能描述出整个系统的优劣，比如针对下面的Skewed Classes：一个分类问题，如果结果仅有两类y=0和y=1，而且其中一类样本非常多，另一类非常少，我们称这种分类问题中的类为Skewed Classes。

EX3：Cancer classification

训练一个逻辑回归模型（$y=1$表示癌症，$y=0$表示没有）来对癌症进行分类，你发现在测试集上的测试误差为1%。

在真实数据中，只有0.5%病人得了癌症。

假设我们设计一个分类器，忽略$x$的数据，对每个病人都认为没有癌症，算法如下：

function y=predictCancer(x)
          y=0; %即忽略x中feature的影响
return;

那么这时的测试误差仅有0.5%。单纯从classification-error来看，比我们之前做的逻辑回归要强，可事实上我们清楚这种cheat方法只是trick，不能用作实际使用。因此，我们引入了Error Metrics。

Precision/Recall

首先给出定义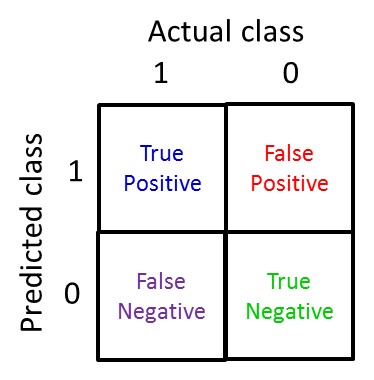： precision & recall 一个二分问题，将实例分成正类（positive）或负类（negative）。对一个二分问题来说，会出现四种情况。如果一个实例是正类并且也被预测成正类，即为真正类（True positive）；如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如果实例是负类被预测成负类，称之为真负类（True negative）；正类被预测成负类则为假负类（false negative）。

通过上面的分类，我们就可以计算准确率（Precision）和召回率（Recall）了：

$\text{Precision} = \frac{\text{True positives}}{\text{# predicted as positive}} = \frac{\text{True positives}}{\text{True positives + False positives}}$ $\text{Recall} = \frac{\text{True positives}}{\text{# actual positives}} = \frac{\text{True positives}}{\text{True positives + False negatives}}$

准确率和召回率的实际含义：

准确率：正确预测正样本/预测为正样本的；
召回率：正确预测正样本/真实值为正样本的；当且仅当准确率和召回率都高的时候我们可以确信，该算法work well !

有了准确率和召回率之后，让我们来分析一下上面的例子： precision/recall example 在前面的例子中，由于TP恒为0，因此准确率和召回率均为0，所以这种算法不可行。

注意：在二分类问题中，正类指定为类中sample较少的那一类，另一类作为false

3.4 Trading off Precison&Recall

EX4：Change the threshold

在前面的癌症分类例子中，通常我们不会将逻辑回归的阈值设定为0.5，因为告诉病人得了癌症是一件非常严重的事情，我们希望在非常确信的情况下才预测为真，因此我们将阈值上调至0.7。

此时的准确率和召回率与之前相比，准确率更高了，因为只有在非常确信的情况下才预测为真；同时召回率下降了，因为真实得癌症的病人可能不会被检测出来。
但是，当我们想尽可能避免出现漏判的情况（即得了癌症的病人没有检测出来，避免假负类（false negative））的时候，这时的阈值需要下调，比如0.3。

此时的召回率更高了，但是准确率下降了。

通常情况下，准确率和召回率两者不能兼得，我们可以画出不同阈值下的准确率和召回率曲线： ROC

F1-score

那么在不同算法或不同阈值造成的不同准确率和召回率之间，我们怎样选择最优算法呢？ compare P&R

这时我们需要定义一个单一的评价标准来同时衡量这两个指标。

最简单的想法是：平均这两个指标：$\frac{P+R}{2}$ average P&R 但是可以看到，与之前用分类精度（accuracy）的弊病类似，如果我们每次都预测为真，那么得到的平均P&R最高，但是很明显这种算法不可行。

因此我们需要一种度量方法，不仅同时考虑P&R，而且避免出现极值情况（一个特别高另一个特别低）。这就引入了F1 score：

$F_1 \text{ Score: }2\frac{PR}{P+R}$

使用F1 score来衡量上面的算法，我们可以得出第一种算法最优的结论，它同时保证了P&R都不能太低。

因此我们可以通过F1 score来自动选择最优的阈值。

3.5 Data for Machine Learning

我们上面讨论了许多算法选择的方法，但在实际使用中，很多时候数据量的大小对于机器学习系统性能的影响要远大于算法的选择。 data size-accuracy 比如在上面这个例子中，可以看到不管选择哪种算法，性能的提升都主要取决于训练集的大小。因此有了下面这句名言：”It’s not who has the best algorithm that wins. It’s who has the most data.”

那么什么时候数据量会对性能产生这么大的影响呢？

Large data rationale

large data rationale 如果特征以及包含了能够正确预测的足够多的信息，那么此时增加数据量对性能的提升肯定是会有帮助；相反，如果特征中只包含了少量的信息，这些信息不足以预测出正确的结果，那么盲目增加数据量就不一定会提升性能。

那么如何来检测是否包含足够的信息呢？可以思考给定输入$x$，一个人类专家能够自信的预测出$y$？如果能，那么信息是足够的，否则可能不够。

large data-low variance

想要保证bias小，就要保证有足够多的feature，即linear/logistics regression中有很多parameters，neuron networks中应该有很多hidden layer neurons；
想要保证variance小，就要保证不产生overfit，那么就需要很多data set。这里需要J(train)和J(CV)都很小，才能使J(test)相对小。

Life

LEGO sets wanted