机器学习课程笔记-5

2017-03-26

Notes about Andrew Ng's Machine Learning course on Coursera-part 5

原创文章，转载请注明：转自Luozm's Blog

1. Neural Networks–Learning

1.1 Cost function

$L$ = 网络层数 $s_l$ =l层的神经元数目（不包括偏置项） $K$ = 输出类别数

Classification

Cost function for NN:

\begin{matrix} J (Θ) = - \frac{1}{m} m \sum i = 1 K \sum k = 1 [y_{k}^{(i)} log ((h_{Θ} (x^{(i)}))_{k}) + (1 - y_{k}^{(i)}) log (1 - (h_{Θ} (x^{(i)}))_{k})] + \frac{λ}{2 m} L - 1 \sum l = 1 s_{l} \sum i = 1 s_{l + 1} \sum j = 1 (Θ_{j, i}^{(l)})^{2} \end{matrix}

$\begin{gather*} J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2\end{gather*}$

其中， $h_\theta(x)\in\mathcal R^K$ ， $(h_\theta(x))_i=i^{th}$ 输出。

1.2 Backpropagation

如何对每个参数求偏导？也就是 $\dfrac{\partial}{\partial \Theta_{i,j}^{(l)}}J(\Theta)$

BP algorithm 具体步骤：准备工作：给定训练集 $\lbrace (x^{(1)}, y^{(1)}) \cdots (x^{(m)}, y^{(m)})\rbrace$ ，对于所有的 $(l,i,j)$ ，令 $\Delta^{(l)}_{i,j}=0$

For 训练样本 t=1 to m：

令 $a^{(1)} := x^{(t)}$
对于 $l=2,3,…,L$ ，正向计算所有输出 $a^{(l)}$
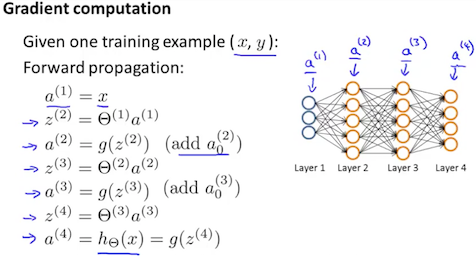
使用 $y^{(t)}$ 来计算 $\delta^{(L)} = a^{(L)} - y^{(t)}$ （这是输出层的误差）
使用 $\delta^{(l)} = ((\Theta^{(l)})^T \delta^{(l+1)}).* a^{(l)}.* (1 - a^{(l)})$ （也就是每层线性组合及sigmoid的局部偏导数）来计算 $\delta^{(L-1)}, \delta^{(L-2)},\dots,\delta^{(2)}$
$\Delta_{i,j}^{(l)}:=\Delta_{i,j}^{(l)}+a_j^{(l)}\delta_i^{(l+1)}$ （或向量版本： $\Delta^{(l)}:=\Delta^{(l)}+\delta^{(l+1)}(a^{(l)})^T$ ）

由此我们更新矩阵：

$D_{i,j}^{(l)} := \dfrac{1}{m}\left(\Delta_{i,j}^{(l)} + \lambda\Theta_{i,j}^{(l)}\right)$ （正则化）

$D_{i,j}^{(l)} := \dfrac{1}{m}\Delta_{i,j}^{(l)}$ （偏置不需要正则化）

最终我们得到： $\frac \partial {\partial \Theta_{ij}^{(l)}} J(\Theta)$

1.3 BP–Intuition

二元分类时：

\begin{matrix} J (Θ) = - \frac{1}{m} m \sum t = 1 K \sum k = 1 [y_{k}^{(t)} log (h_{Θ} (x^{(t)}))_{k} + (1 - y_{k}^{(t)}) log (1 - h_{Θ} (x^{(t)})_{k})] + \frac{λ}{2 m} L - 1 \sum l = 1 s_{l} \sum i = 1 s_{l} + 1 \sum j = 1 (Θ_{j, i}^{(l)})^{2} \end{matrix}

$\begin{gather*}J(\Theta) = - \frac{1}{m} \sum_{t=1}^m\sum_{k=1}^K \left[ y^{(t)}_k \ \log (h_\Theta (x^{(t)}))_k + (1 - y^{(t)}_k)\ \log (1 - h_\Theta(x^{(t)})_k)\right] + \frac{\lambda}{2m}\sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l+1} ( \Theta_{j,i}^{(l)})^2\end{gather*}$

其中一个样本（忽略正则化）：

c o s t (t) = y^{(t)} log (h_{Θ} (x^{(t)})) + (1 - y^{(t)}) log (1 - h_{Θ} (x^{(t)}))

$cost(t) =y^{(t)} \ \log (h_\Theta (x^{(t)})) + (1 - y^{(t)})\ \log (1 - h_\Theta(x^{(t)}))$

最后一层的误差正式地说应该是损失函数对于scores function的偏导数： $\delta_j^{(l)} = \dfrac{\partial}{\partial z_j^{(l)}} cost(t)$

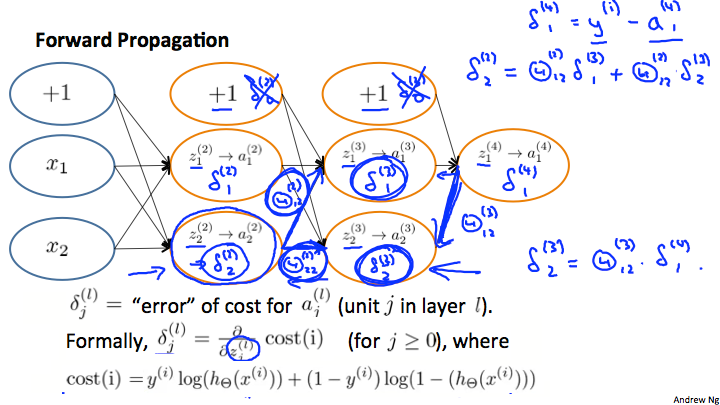
bp_intuition

注意有分支结构时，反向传播求导应该相加： $\delta_2^{(2)}=\Theta_{12}^{(2)}*\delta_1^{(3)}+\Theta_{22}^{(2)}*\delta_2^{(3)}$

Life

LEGO sets wanted