DBN原理及实践总结-1

2017-03-03

深度信念网络原理、实践及相关技巧总结

原创文章，转载请注明：转自Luozm's Blog

深度信念网络（Deep Belief Networks，DBN）是一种概率生成模型，是多个受限玻尔兹曼机（Restricted Boltzmann Machines，RBM）的堆叠，其中每个RBM层与其上下两层相连，且任意层内的单元不相互连接。除了第一层和最后一层之外，DBN的每一层都有两个作用：作为前一层的隐藏层，或者作为后一层的输入（可视层）。堆叠的RBM层上可以连接一个Softmax层来将整个DBN当做分类器使用，也可以简单的在无监督学习中用于无标签数据的聚类。DBN通常用于识别，聚类和生成图像、影像序列或者动作捕捉，由Geoff Hinton和他的学生在2006年首次提出。

本文大部分内容翻译自 DeepLearning 0.1 documentation¹，也参考了许多文献和博客的内容。

1.1 Discriminative/Generative Model

判别模型（Discriminative Model，DM），又可以称为条件模型，或条件概率模型。估计的是条件概率分布(conditional distribution)，即 $P(y|x)$。因为没有 $x$ 的知识，无法生成样本，只能判断分类。
生成模型（Generative Model，GM），又叫产生式模型。估计的是联合概率分布（joint probability distribution），即 $P(x,y)=P(y|x)×P(x)$。因为知道 $x,y$ 的联合分布，因此可以根据概率来生成样本。

举例来说，两种典型的算法朴素贝叶斯（Naive Bayes）和逻辑回归（Logistic Regression）实际上就分别是GM和DM的两种最基本的算法。

详细分析可见pluskid’s Blog²、Fishmemory的博客³和Andrew Ng的论文⁴。

1.2 Probabilistic Graphical Model

概率图模型（Probabilistic Graphical Model，PGM）使用一种基于图的表示来编码高维空间中的复杂联合概率分布。概率图模型的目的是提供一种机制能够利用复杂分布的结构来简洁地描述它们,并能有效地构造和利用它们。

将图模型引入概率分布的好处⁵：

They provide a simple way to visualize the structure of a probabilistic model and can be used to design and motivate new models.
Insights into the properties of the model, including conditional independence properties, can be obtained by inspection of the graph.
Complex computations, required to perform inference and learning in sophisticated models, can be expressed in terms of graphical manipulations, in which underlying mathematical expressions are carried along implicitly.

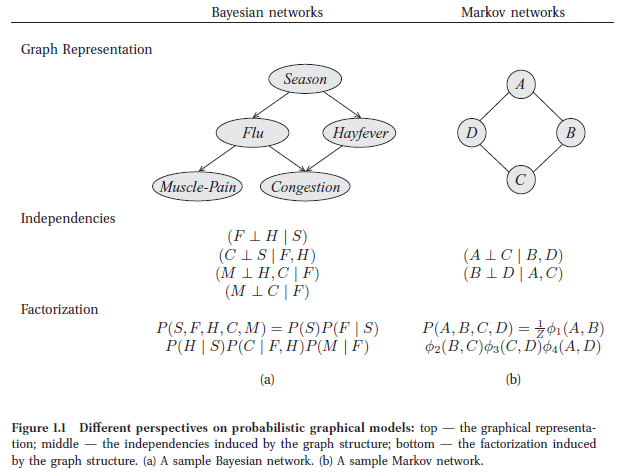
在基于图的表示中（如下图所示），节点（nodes/ovals）对应于变量，边（edges）对应于变量间的直接概率关系。 Graph Representation

基本的PGM可以大致分为两个类别：贝叶斯网络（Bayesian Network，BN）和马尔可夫随机场（Markov Random Field，MRF）。它们的主要区别在于采用不同类型的图来表达变量之间的关系：

贝叶斯网络采用有向无环图（Directed Acyclic Graph）来表达因果关系。一般来说，贝叶斯网络中每一个节点都对应于一个先验概率分布或者条件概率分布，因此整体的联合分布可以直接分解为所有单个节点所对应的分布的乘积。
马尔可夫随机场则采用无向图（Undirected Graph）来表达变量间的相互作用。对于马尔可夫场，由于变量之间没有明确的因果关系，它的联合概率分布通常会表达为一系列势函数（potential function）的乘积。通常情况下，这些乘积的积分并不等于1，因此，还要对其进行归一化才能形成一个有效的概率分布——这一点往往在实际应用中给参数估计造成非常大的困难。

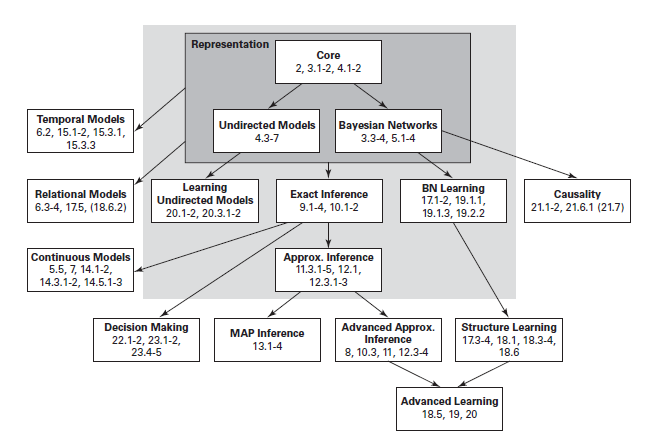
概率图模型主要有三个关注点：

图模型的表示（representation）：指的是一个图模型应该是什么样子的；
图模型的推断（inference）：指的是已知图模型的情况下，怎么去计算一个查询的概率，例如已经一些观察节点，去求其它未知节点的概率；
图模型的学习（learning）：这里又分为两类，一类是图的结构学习；一类是图的参数学习。

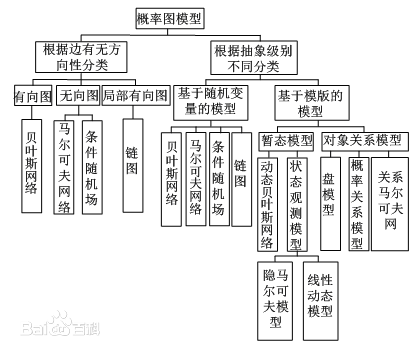
概率图模型的理论体系如下⁶： PGM Roadmap

简单中文介绍可见 暗海风的博客 ⁷ 或 码农场⁸。

1.3 Energy-Based Models

能量模型（Energy-Based Models，EBM）把我们所关心变量的各种组合和一个标量能量联系在一起。我们训练模型的过程就是不断改变标量能量的过程。比如，如果一个变量组合被认为是合理的，它同时也具有较小的能量。基于能量的概率模型通过能量函数定义概率分布，如下：

$p(x)=\frac{e^{-E(x)}}{Z}$

其中Z为归一化因子，类比于统计物理学中的配分函数（Partition Function）：

$Z=\sum_xe^{-E(x)}$

能量模型可以利用使用（随机）梯度下降的方法来学习，具体而言，就是以训练集的负对数似然函数作为损失函数：

$\mathcal l(\theta,\mathcal D)=-\mathcal L(\theta,\mathcal D)=-\frac{1}{N}\sum_{x^{(i)}\in\mathcal D}\log p(x^{(i)})$

其中θ为模型的参数，使用随机梯度 $-\frac{\partial\log p(x^{(i)})}{\partial\theta}$ 来训练。

EBMs with Hidden Units

在很多情况下，我们无法观察到样本的所有属性，或者我们需要引进一些没有观察到的变量，以增加模型的表达能力。考虑一个观察到的部分 $x$ 和一个隐含部分 $h$ ：

$P(x)=\sum_hP(x,h)=\sum_h\frac{e^{-E(x,h)}}{Z}$

在这种情况下，为了与不包含隐含变量的模型进行统一，我们引入如下的自由能量函数：

$\mathcal F(x)=-\log\sum_he^{-E(x,h)}$

于是 $P(x)$ 就可以写成：

$P(x)=\frac{e^{-\mathcal F(x)}}{Z}$

其中 $Z=\sum_xe^{-\mathcal F(x)}$ 。

此时，损失函数还是类似的定义，只是在进行梯度下降求解时稍微有些不同：

$\begin{aligned} -\frac{\partial\log p(x)}{\partial\theta} &=-\frac{\partial(-\mathcal F(x)-\log Z)}{\partial\theta}\\ &=\frac{\partial\mathcal F(x)}{\partial\theta}+\frac{\partial\log Z}{\partial\theta}\\ &=\frac{\partial\mathcal F(x)}{\partial\theta}+\frac{1}{Z}\frac{\partial Z}{\partial\theta}\\ &=\frac{\partial\mathcal F(x)}{\partial\theta}-\frac{1}{Z}(\sum_xe^{-\mathcal F(x)}\frac{\partial\mathcal F(x)}{\partial\theta})\\ &=\frac{\partial\mathcal F(x)}{\partial\theta}-(\frac{\sum_xe^{-\mathcal F(x)}}{Z}\frac{\partial\mathcal F(x)}{\partial\theta})\\ &=\frac{\partial\mathcal F(x)}{\partial\theta}-(\sum_\tilde xP(\tilde x)\frac{\partial\mathcal F(\tilde x)}{\partial\theta}) \end {aligned}$

中间过程可能有误

该梯度表达式中包含两项，他们都影响着模型所定义的概率密度：第一项增加训练数据的概率（通过减小对应的自由能量），而第二项则减小模型生成的样本的概率。

通常，我们很难精确计算这个梯度，因为式中第一项涉及到计算 $E_p[\frac{\partial\mathcal F(x)}{\partial\theta}]$，这是对输入 $x$ 的所有可能组合的期望（在模型生成的分布 $p$ 下）。

使这个计算易于处理的第一步是使用固定数目的模型样本估计期望。用于估计负数项梯度的样本称为负粒子（negative particles），它们记为 $\mathcal N$。梯度可以写成如下形式：

$-\frac{\partial\log p(x)}{\partial\theta}\approx\frac{\partial\mathcal F(x)}{\partial\theta}-\frac{1}{|\mathcal N|}\sum_{\tilde x\in\mathcal N}\frac{\partial\mathcal F(\tilde x)}{\partial\theta}$

在理想情况下，我们将 $\mathcal N$ 中的元素 $\tilde x$ 根据 $P$ 取样（即蒙特卡罗，Monte-Carlo）。利用上述公式，我们几乎得到一个实际的随机算法来学习EBM。唯一缺少的部分是如何提取这些负粒子 $\mathcal N$。虽然统计文献中有大量的抽样方法，但马尔可夫链蒙特卡罗方法（Markov Chain Monte Carlo，MCMC）特别适用于例如RBM（一种特殊类型的EBM）一类的模型。

详细资料可见 Vincent乐的博客⁹。

2. Restricted Boltzmann Machines

2.1 Boltzmann Machines

波尔兹曼机（Boltzmann Machines，BM）是Hinton和Sejnowski于1986年提出的一种源自统计力学的随机神经网络。这种网络中的神经元是随机神经元，神经元的输出只有两种状态（未激活、激活），一般用二进制的0和1表示，状态的取值根据概率统计法则决定。从功能上讲，BM是由随机神经元全连接组成的反馈神经网络，且对称连接，无自反馈，如图所示：

波尔兹曼机是一种特殊形式的对数线性的马尔可夫随机场，即能量函数是自由变量的线性函数。通过引入隐含变量，我们可以提升模型的表达能力，表示非常复杂的概率分布。

包含一个可见层和一个隐层的BM模型如下左图所示： BM&RBM

2.2 Restricted Boltzmann Machines

RBM如上右图所示，是一种特殊形式的玻尔兹曼机，由一个可视层（一般用 $v$ 表示）和一个隐含层（一般用 $h$ 表示）组成。只有可见层节点和隐含层节点有连接权值，而每一层的节点之间没有链接。已知 $v$ 的情况下，所有的隐藏节点之间是条件独立的。输入 $v$ 时，通过条件概率可以得到隐藏层 $h$ ，同理，根据隐藏层 $h$ 可以得到可视层 $v$ 。对参数进行调整后，如果从隐藏层得到的可视层 $v’$ 与原来的可视层 $v$ 一致，那么得到的隐藏层就是可视层另外一种表示。

RBM的能量函数 $E(v,h)$ 定义为：

$E(v,h)=−b′v−c′h−h′Wv$

其中$’$表示转置，$b,c,W$ 为模型的参数，$b,c$ 分别为可见层和隐含层的偏置，$W$ 为可见层与隐含层的链接权重。此时，对应的自由能量为：

$\mathcal F(v)=-b'v-\sum_i\log\sum_{h_i}e^{h_i(c_i+W_iv)}$

另外，由于RBM的特殊结构，可见层/隐含层内个单元之间是相互独立的，所以我们有：

$p(h\|v)=\prod_ip(h_i\|v)$ $p(v\|h)=\prod_jp(v_j\|h)$

RBMs with binary units

如果RBM中的每个单元都是二值的，即 $v_j,h_i∈{0,1}$，概率版本的常见激活函数为：

$P(h_i=1\|v)=sigm(c_i+W_iv)$ $P(v_j=1\|h)=sigm(b_j+W^{'}_jh)$

自由能量函数简化为：

$\mathcal F(v)=-b'v-\sum_i\log(1+e^{(c_i+W_iv)})$

Update Equations with Binary Units

使用梯度下降法求解模型参数时，各参数的对数似然梯度如下：

$\begin {aligned} -\frac{\partial\log p(v)}{\partial W_{ij}}&=E_v[p(h_i\|v)\cdot v_j]-v^{(i)}_j\cdot sigm(W_i\cdot v^{(i)}+c_i)\\ -\frac{\partial\log p(v)}{\partial c_{i}}&=E_v[p(h_i\|v)]-sigm(W_i\cdot v^{(i)})\\ -\frac{\partial\log p(v)}{\partial b_{j}}&=E_v[p(v_j\|h)]-v^{(i)}_j \end {aligned}$

详细推导可见 Contrastive divergence multi-layer RBMs¹⁰ 或 Learning Deep Architectures for AI ¹¹的第5节。

2.3 Sampling in an RBM (Training)

前面提到了，RBM是很难学习的，即模型的参数很难确定，下面我们就具体讨论一下基于采样的近似学习方法。学习RBM的任务是求出模型的参数 $\theta={c,b,W}$的值。

关于MCMC及Gibbs采样，强烈推荐阅读：LDA-math-MCMC 和 Gibbs Sampling(1)(2) ¹²。

Gibbs sampling

Gibbs采样是一种基于MCMC的采样方法。对于一个 $K$ 维随机变量 $X=(X_1,X_2,\dots,X_K)$，假设我们无法求得联合分布 $P(X)$，但我们知道给定 $X$ 的其他分量时，其第 $k$ 个分量 $X_k$ 的条件分布，即 $P(X_k|X_{k−})$，其中 $X_{k−}=(X_1,X_2,\dots,X_{k−1},X_{k+1},\dots,X_K)$。那么，我们可以从 $X$ 的一个任意状态（比如 $[x_1(0),x_2(0),\dots,x_K(0)]$ ）开始，利用上述条件分布，迭代的对其分量依次采样。随着采样次数的增加，随机变量 $[x_1(n),x_2(n),\dots,x_K(n)]$ 的概率分布将以 $n$ 的几何级数的速度收敛于 $X$ 的联合概率分布 $P(X)$。也就是说，我们可以在未知联合概率分布的条件下对其进行采样。

对于RBM,$X$ 包括一组可视和隐含的单元。然而,由于它们条件独立,可以执行分块Gibbs抽样。在该设置中，给定隐藏单元的同时采样可见单元。类似地，在给定可见的同时采样隐藏单元。因此，马尔可夫链中的一步采样如下：

$\begin{aligned} h^{(n+1)}&\sim sigm(W'v^{(n)}+c)\\ v^{(n+1)}&\sim sigm(Wh^{(n+1)}+b) \end{aligned}$

其中 $h^{(n)}$ 表示第 $n$ 步采样中的所有隐含单元的集合。它的意思是，举例来说，$h^{(n+1)}_i$ 根据概率 $sigm(W^{‘}_iv^{(n)}+c_i)$ 随机给定值1（vs 0），同样地，$v^{(n+1)}_j$ 根据概率 $sigm(W_jh^{(n+1)}+b_j)$ 随机给定值1（vs 0）。迭代过程如下图所示： Gibbs Step

在步数 $k$ 足够大的情况下，我们可以得到服从RBM所定义的分布的样本。

在理论上，学习过程中的每个参数更新都需要运行一个这样的链来收敛。不用说，这样做会使人望而却步。为此，人们设计了几种算法，以便在学习过程中有效地从 $p(v,h)$ 采样。

Contrastive Divergence (CD-k)

2002年，Hinton¹³提出了RBM的一个快速学习算法，即对比散度（Contrastive Divergence，CD）算法，它使用了两个技巧来加速采样过程：

因为我们最终想得到 $p(v)\approx p_{train}(v)$（数据的真实分布），我们用训练样本来初始化马尔可夫链（即从一个预期接近 $p$ 的分布开始，使得初始链已经接近收敛到最终分布 $p$）。
CD不等待迭代链收敛。样本仅仅经Gibbs采样 $k$ 步得到。在实践中，$k=1$ 时的结果就已经很出色了。

RBM的基于CD的快速学习算法主要步骤如下：

上述基于CD的学习算法是针对RBM的可见单元和隐层单元均为二值变量的情形，我们可以很容易的推广到可见单元和隐单元为高斯变量的情形。

Persistent CD

Persistent CD¹⁴使用另一种近似来从 $p(v,h)$ 中取样。它依赖于一个简单的具有持久状态（persistent state，即不为每个观察到的例子重新开始一个链）的马尔可夫链。对于每个参数更新，我们通过简单地运行这个链 $k$ 步来提取新的样本。然后保存链的状态以用于后续更新。

一般的直觉是，如果参数更新的速度与链的混合速率相比足够小，那么马尔可夫链应该能够“跟上”模型的变化。

2.4 Implementation & Tricks

Applications

RBM的用途主要有四种：

第一种是对数据进行编码，然后交给监督学习方法去进行分类或回归，也就是把它当做降维或者特征提取的方法来使用；
第二种是得到了权重矩阵和偏移量，供BP神经网络初始化训练。原因是神经网络也是要训练一个权重矩阵和偏移量，但是如果直接用BP神经网络，初始值选得不好的话，往往会陷入局部极小值。根据实际应用结果表明，直接把RBM训练得到的权重矩阵和偏移量作为BP神经网络初始值，得到的结果会非常地好;
第三种，RBM可以作为一个生成模型使用。RBM可以估计联合概率 $p(v,h)$，如果把 $v$ 当做训练样本，$h$ 当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为1的概率），就可以利用利用贝叶斯公式求 $p(h|v)$，然后就可以进行分类，类似朴素贝叶斯、LDA、HMM；
第四种，RBM可以作为一个判别模型使用。RBM可以直接计算条件概率 $p(h|v)$，如果把 $v$ 当做训练样本，$h$ 当成类别标签（隐藏节点只有一个的情况，能得到一个隐藏节点取值为1的概率），RBM就可以用来进行分类。

后续部分未完成，见http://deeplearning.net/tutorial/rbm.html#implementation

Implementation

Tricks

更多资料可查看¹⁵¹⁶，关于能量函数和概率公式的推导，可以参考 深度学习读书笔记之RBM¹⁷。

References

DeepLearning 0.1 documentation, Restricted Boltzmann Machines (RBM) ↩
pluskid’s Blog, Discriminative Modeling vs Generative Modeling ↩
Fishmemory的博客, 判别模型(Discriminative model)和生成模型(Generative model) ↩
Ng A Y, Jordan M I. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes[J]. Advances in neural information processing systems, 2002, 2: 841-848. ↩
Bishop C M. Pattern Recognition and Machine Learning (Information Science and Statistics)[M]. Springer-Verlag New York, Inc. 2006. ↩
Koller D, Friedman N. Probabilistic graphical models: principles and techniques[M]. MIT press, 2009. ↩
暗海风的博客, 概率图模型 ↩
码农场, 条件随机场 ↩
Vincent乐的博客, 能量模型(EBM)、限制波尔兹曼机(RBM) ↩
LISA, Contrastive divergence multi-layer RBMs ↩
Bengio Y. Learning deep architectures for AI[J]. Foundations and trends® in Machine Learning, 2009, 2(1): 1-127. ↩
rickjin的博客, LDA-math-MCMC 和 Gibbs Sampling(1)、LDA-math-MCMC 和 Gibbs Sampling(2) ↩
Hinton G E. Training products of experts by minimizing contrastive divergence[J]. Neural computation, 2002, 14(8): 1771-1800. ↩
Tieleman T. Training restricted Boltzmann machines using approximations to the likelihood gradient[C]. Proceedings of the 25th international conference on Machine learning. ACM, 2008: 1064-1071. ↩
Fischer A, Igel C. An introduction to restricted Boltzmann machines[C]. Iberoamerican Congress on Pattern Recognition. Springer Berlin Heidelberg, 2012: 14-36. ↩
Hinton G. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2010, 9(1): 926. ↩
falao_beiliu的博客, 深度学习读书笔记之RBM ↩

Life

LEGO sets wanted

DBN原理及实践总结-1

1.1 Discriminative/Generative Model

1.2 Probabilistic Graphical Model

1.3 Energy-Based Models

EBMs with Hidden Units

2. Restricted Boltzmann Machines

2.1 Boltzmann Machines

2.2 Restricted Boltzmann Machines

RBMs with binary units

Update Equations with Binary Units

2.3 Sampling in an RBM (Training)

Gibbs sampling

Contrastive Divergence (CD-k)

Persistent CD

2.4 Implementation & Tricks

Applications

Implementation

Tricks

References

Life

Theory

Develop

DBN原理及实践总结-1

1. Related Concepts

1.1 Discriminative/Generative Model

1.2 Probabilistic Graphical Model

1.3 Energy-Based Models

EBMs with Hidden Units

2. Restricted Boltzmann Machines

2.1 Boltzmann Machines

2.2 Restricted Boltzmann Machines

RBMs with binary units

Update Equations with Binary Units

2.3 Sampling in an RBM (Training)

Gibbs sampling

Contrastive Divergence (CD-k)

Persistent CD

2.4 Implementation & Tricks

Applications

Implementation

Tricks

References

Life

Theory

Develop